What is number system in Hindi ?
संख्या पद्धति (Number System in Hindi) – अंकों के द्वारा संख्याएं बनाने, संख्याओं को लिखने तथा उनके नामकरण की सुव्यवस्थित व क्रमबद्ध पद्धति और विभिन्न संख्याओं एवं उनके मध्य सम्बन्धों व नियमों के क्रमबद्ध अध्ययन को संख्या पद्धति (Number System In Hindi) कहा जाता है।
संख्या पद्धति मुख्यतः कितने प्रकार की है? (Types of number system in Hindi) – संख्या पद्धति को मुख्य रूप से दो प्रणालियों में पढ़ा जाता है।
(1) दाशमिक संख्या प्रणाली (Decimal Number System In Hindi) – हमारे प्रतिदिन के कार्यों में जिस संख्या प्रणाली का प्रयोग होता है, उसे लिखने या दर्शाने के लिए (0, 1, 2, 3, 4, 5, 6, 7, 8 और 9) संकेतों का प्रयोग किया जाता है। चूँकि इस पद्धति में संख्याओं को लिखने के लिए 10 संकेतों का प्रयोग किया जाता है, इसलिए इस संख्या पद्धति को दाशमिक संख्या प्रणाली कहते हैं।
नोट : दाशमिक संख्या प्रणाली को हिंदू-अरैबिक प्रणाली भी कहते हैं।
दाशमिक संख्या प्रणाली की विशेषताएं (Characters of Decimal Number System In Hindi) – दाशमिक संख्या प्रणाली के मुख्य विशेषताएं निम्नलिखित हैं-
- इसमें संख्याओं को लिखने के लिए 10 संकेतों (0, 1, 2, 3, 4, 5, 6, 7, 8 और 9) का प्रयोग होता है।
- इसमें संख्याओं को लिखने के लिए दाएं ओर से बाएं ओर स्थानीय मान क्रमशः इकाई, दहाई, सैकड़ा, हजार, दस हजार, लाख, दस लाख,… इत्यादि होते हैं।
- इसमें दाएं ओर से बाएं ओर क्रमशः जितना आगे बढ़ते हैं, उतना ही अंकों के स्थानीय मान में 10 गुना (दस गुना) वृद्धि होती है।
(2) रोमन संख्या प्रणाली (Roman Number System In Hindi) – रोमन संख्याओं को अंग्रेजी वर्णमाला के अक्षरों से प्रदर्शित किया जाता है। जैसे I, V, X आदि।
रोमन संख्यायें लिखने के नियम –
(a) यदि किसी संकेत की पुनरावृत्ति (दो बार) होती है, तो जितनी बार वह आता है उसका मान उतनी ही बार जोड़ दिया जाता है।
उदाहरण – ll = 2 (1+1), XX = 20 (10+10), XXX = 30 (10+10+10)
(b) कोई संकेत तीन से अधिक बार नहीं लिखा जाता है। परंतु V, L और D संकेतों की कभी पुनरावृत्ति नहीं होती है।
(c) यदि छोटे मान वाला कोई संकेत एक बड़े मान वाले संकेत के दाईं ओर लिखा जाता है, तो बड़े मान में छोटे मान को जोड़ दिया जाता है।
उदाहरण – VI = 5 + 1 = 6, XII = 10 + 2 = 12, XV = 10 + 5 = 15
(d) यदि छोटे मान वाला कोई संकेत बड़े मान वाले किसी संकेत के बाईं ओर आता है, तो बड़े मान में से छोटे मान को घटा दिया जाता है। उदाहरण – IV = 5 – 1 = 4, IX = 10 – 1 = 9, XL = 50 – 10 = 40, XC = 100 – 10 = 90
(e) V, L और D संकेतों को कभी भी बड़े मान वाले संकेत के बाईं ओर नहीं लिखा जाता है। अर्थात् V, L और D के मानों को कभी भी घटाया नहीं जाता है।
(f) संकेत I को केवल V और X में से घटाया जा सकता है। संकेत X को केवल L, M और C में से ही घटाया जा सकता है।
संख्यांक का शाब्दिक अर्थ – संख्यांक का शाब्दिक अर्थ है संख्या + अंक। अर्थात् संख्या को लिखने के लिए प्रयुक्त होने वाले अंक।
उदाहरण – 1, 12, 27 आदि।
अंक या संख्यांक की परिभाषा (Definition of Digits) – संख्याओं को जिन संकेतों द्वारा व्यक्त करते हैं, उन्हें अंक या संख्यांक कहते हैं।
उदाहरण – 1, 2, 3, 4, 5 आदि।
गणित में कितने अंक प्रयोग होते हैं ?
अंक 10 होते हैं – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
अंकों के मान (Value of Digit) – किसी संख्या में प्रत्येक स्थान के संगत अंक का मान अलग अलग होता है। किसी भी संख्या में प्रयोग की जाने वाले अंक के दो मान होते हैं।
- वास्तविक मान (Face Value)
- स्थानीय मान (Place Value)
वास्तविक मान की परिभाषा (Face Value Definition) – किसी भी संख्या में प्रयुक्त अंक का वास्तविक मान वह अंक स्वयं ही होता है चाहे वह किसी भी स्थान पर प्रयोग हो अर्थात किसी भी संख्या में प्रयुक्त अंक का वास्तविक मान हमेशा स्थाई (स्थिर) होता है।
नोट : वास्तविक मान को अंकित मान, शुद्ध मान या जातीय मान भी कहते हैं।
उदाहरण – संख्या 6269 मे ‘6’ का वास्तविक मान या अंकित मान दोनों स्थानों पर 6 ही होगा।
स्थानीय मान की परिभाषा (Place Value Definition) – किसी भी संख्या में प्रयुक्त अंक का स्थानीय मान वह होता है जिस स्थान पर उस अंक को लिखा जाता है। अथवा किसी अंक का वह मान जो उसके स्थान विशेष के कारण होता है, उस अंक का स्थानीय मान कहलाता है।
उदाहरण – (1) संख्या 5732 का स्थानीय मान ज्ञात कीजिए।
हल – 5327 = 5×1000 + 7×100 + 3×10 + 2×1
= 5000 + 700 + 30 + 2
= 5732
उदाहरण – (2) संख्या 9727 में केवल 7 का स्थानीय मान ज्ञात कीजिए।
हल – संख्या 7127 मे प्रथम 7 का स्थानीय मान = 7×1 = 7
तथा द्वितीय 7 का स्थानीय मान = 7×100 = 700
निष्कर्ष – अतः स्पष्ट है किसी संख्या में एक से अधिक बार आए अंक का वास्तविक मान तो समान होगा, जबकि स्थानीय मान भिन्न होंगे।
भारतीय संख्या पद्धति (Indian Number System) – भारतीय संख्या पद्धति के अनुसार संख्याओं को लिखने के लिए दायीं से बायीं ओर क्रमशः इकाई, दहाई, सैकड़ा, हजार, दस हजार, लाख, दस लाख, करोड़, दस करोड़, अरब, दस अरब, खरब, दस खरब, नील, दस नील, पदम, दस पदम, शंख, दस शंख, महाशंख आदि स्थानों का प्रयोग होता है।
अंतर्राष्ट्रीय संख्याएं (International Number System in Hindi) – अंतरराष्ट्रीय संख्याएं भी दायीं से बायीं ओर लिखी जाती हैं परंतु इन्हें अलग नाम क्रमशः इकाई, दहाई, सैकड़ा, हजार, दस हजार, सौ हजार, मिलियन, दस मिलियन, बिलियन इत्यादि नामों से जाना जाता है।
शून्य (Zero) – इसका संकेत ‘0’ है तथा यह सबसे छोटा अंक है। शून्य का अकेले में कोई अस्तित्व नहीं है।
शून्य से संबंधित कुछ रोचक तथ्य –
- किसी संख्या में शून्य जोड़ने या घटाने पर संख्या के मान मे कोई प्रभाव नहीं पड़ता है।
- किसी संख्या में शून्य का गुणा करने पर गुणनफल हमेशा शून्य ही आता है।
- शून्य का किसी संख्या में भाग अपरिभाषित है।
- शून्य को किसी संख्या के बायीं ओर लिखने पर संख्या के मान पर कोई प्रभाव नहीं पड़ता है परंतु दायीं ओर लिखने पर संख्या के मान में 10 गुना वृद्धि हो जाती है।
- शून्य का शून्य से गुणा या भाग अपरिभाषित है।
शून्येत्तर संख्याएं (Non-Zero Numbers) – शून्य को छोड़कर अन्य सभी अंको को शून्येत्तर संख्याएं कहते हैं।
संख्या (Number) – “कितनी वस्तुएँ हैं” का जिससे बोध होता है, उसे संख्या कहते हैं।
अथवा
एक, दो या दो से अधिक अंको के मिलने से प्राप्त व्यंजक को, संख्या कहते हैं।
उदाहरण – 7, 13, 245 … आदि।
नोट – संख्याएँ अनंत होती हैं।
गिनती की संख्याएँ (Counting Numbers) – वस्तुओं को गिनने के लिए जिन इकाइयों या संख्याओं का प्रयोग करते हैं, उन्हें गिनती की संख्याएँ कहते हैं। उदाहरण – 1, 2, 3, 4, 5, 6, 7, 8, 9, …∞ (अनंत) आदि।
प्राकृत या प्राकृतिक संख्याएँ (Naturals Numbers) – गणना या गिनती कि संख्याओं (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …) को, प्राकृत या प्राकृतिक संख्याएँ कहते हैं। प्राकृतिक संख्याओं को N या n से प्रदर्शित करते हैं।
अथवा
प्राकृतिक संख्या वह संख्या है जो 1 से शुरू होकर अपरिमित (जिसकी कोई सीमा ना हो) रूप से बढ़ती रहती है।
उदाहरण – N or n = 1, 2, 3, 4, 5, 6, 7, 8, 9, …∞ (अनंत) आदि।
नोट – 1 सबसे छोटी एवं पहली प्राकृतिक संख्या है।
पूर्ववर्ती संख्या (Predecessor Number) – किसी संख्या के ठीक पहले वाली संख्या उस संख्या की पूर्ववर्ती संख्या होती है।
अथवा
किसी भी संख्या में 1 घटाने से उसकी पूर्ववर्ती संख्या प्राप्त हो जाती है।
उदाहरण – निम्नलिखित संख्याओं की पूर्ववर्ती संख्या ज्ञात कीजिए।
(1) 17 (2) 159
हल – (1) 13 की पूर्ववर्ती संख्या = 17-1 = 16
अतः 17 की पूर्ववर्ती संख्या 16 है।
(2) 159 की पूर्ववर्ती संख्या = 159-1 = 158
अतः 159 की पूर्ववर्ती संख्या 158 है।
नोट – 1 की कोई पूर्ववर्ती प्राकृतिक संख्या नहीं होती है। चूँकि पूर्ववर्ती संख्या किसी संख्या के ठीक पहले वाली संख्या को कहते हैं। और हम सभी जानते हैं कि 1 सबसे छोटी और पहली संख्या है। इसलिए एक की कोई पूर्ववर्ती संख्या नहीं होती है।
अनुवर्ती या उत्तरवर्ती संख्या (Successor Numbers) – किसी संख्या के ठीक बाद वाली संख्या उस संख्या कि अनुवर्ती या उत्तरवर्ती संख्या होती हैै। यह परवर्ती संख्या के नाम से भी जाना जाता है।
अथवा
किसी भी संख्या में 1 जोड़ने से उसकी अनुवर्ती या उत्तरवर्ती संख्या प्राप्त होती है।
उदाहरण- संख्या 32 की अनुवर्ती संख्या ज्ञात कीजिए।
हल – 27 की अनुवर्ती संख्या = 27+1 = 28
अतः 27 की अनुवर्ती संख्या 28 है।
नोट – 1 किसी भी प्राकृतिक संख्या की अनुवर्ती प्राकृतिक संख्या नहीं है। कोई भी प्राकृतिक संख्या सबसे बड़ी प्राकृतिक संख्या नहीं होती है क्योंकि उसकी अनुवर्ती संख्या उससे भी बड़ी होती है।
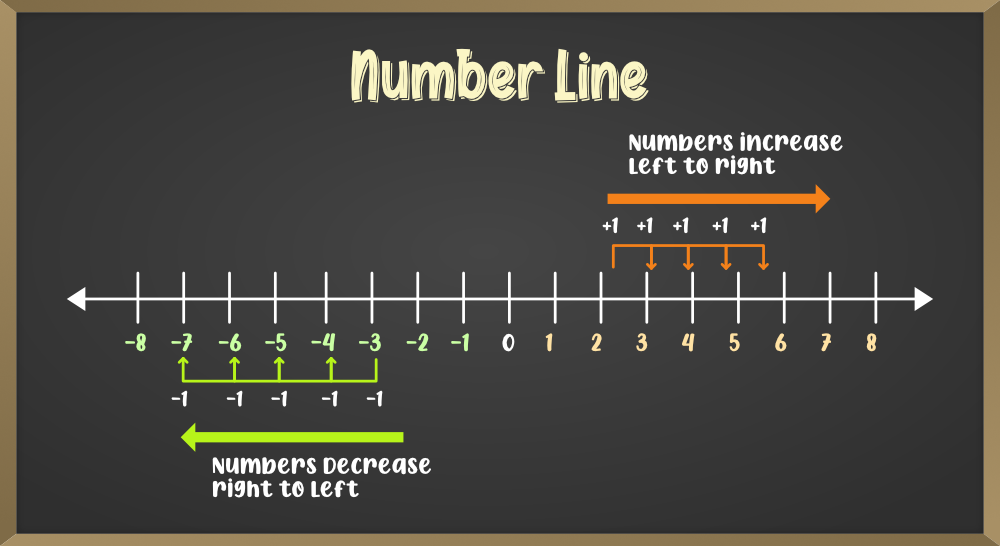
प्राकृतिक संख्याओं का संख्या रेखा पर प्रदर्शन
1. सर्वप्रथम एक रेखा खींचते हैं।
2. फिर उस रेखा पर समान दूरी लेकर उन्हें चिन्हित करते हैं।
3. फिर प्राप्त बिंदुओं के नीचे क्रमशः संख्याएँ 1, 2, 3, 4, 5, 6, 7, 8, 9, … निरूपित करते हैं।
नोट – संख्या रेखा पर प्रत्येक प्राकृतिक संख्या अपनी बायीं ओर की प्रत्येक प्राकृतिक संख्या से बड़ी तथा अपने दायीं ओर के प्रत्येक प्राकृतिक संख्या से छोटी होती है।
आरोही क्रम (Ascending Order) – आरोही क्रम का शाब्दिक अर्थ है – क्रम से आगे बढ़ना। दी गई संख्याओं को बढ़ते क्रम में रखने को, आरोही क्रम कहते हैं। इस क्रम में सबसे पहले सबसे छोटी संख्या, फिर उससे बड़ी संख्या, फिर उससे बड़ी संख्या और अंत में सबसे बड़ी संख्या को क्रमानुसार रखा जाता है।
उदाहरण – संख्याओं 2769, 693, 8253, 399 को आरोही क्रम में लिखिए।
हल – पहले सबसे छोटी संख्या = 399
उसके बाद उससे बड़ी संख्या = 693
उसके बाद उससे बड़ी संख्या = 2769
और अंत में सबसे बड़ी संख्या = 8253
अतः आरोही क्रम = 399, 693, 2769, 8253
अवरोही क्रम का शाब्दिक अर्थ –
अवरोही क्रम (Descending Order) – अवरोही क्रम का शाब्दिक अर्थ है – नीचे उतरना। जब कोई दी गई संख्याओं को घटते क्रम में लिखा जाता है, उसे अवरोही क्रम कहते हैं। इस क्रम में सबसे पहले सबसे बड़ी संख्या, फिर उससे छोटी संख्या, फिर उससे छोटी संख्या और अंत में सबसे छोटी संख्या को क्रमानुसार रखा जाता है।
उदाहरण – संख्याओं 2115, 6502, 2107, 1014 को अवरोही क्रम में लिखिए।
हल – पहले सबसे बड़ी संख्या = 6809
उसके बाद उससे छोटी संख्या = 2345
उसके बाद उससे छोटी संख्या = 2344
और अंत में सबसे छोटी संख्या = 1234
अतः अवरोही क्रम = 6809, 2345, 2344, 1234
प्राकृतिक संख्याओं के क्रम सूचक और मात्रा सूचक
1. क्रम सूचक (Serial indicator) – जिन बातों से हमें क्रम (प्रथम, द्वितीय, तृतीय, …) का बोध होता है, क्रम सूचक कहलाते हैं।
उदाहरणार्थ:- (a) अप्रैल वर्ष का चौथा महीना है।
(b) अरशद ने वार्षिक परीक्षा में प्रथम स्थान प्राप्त किया।
2. मात्रा सूचक (Quantity indicator) – जिन बातों से हमें मात्रा (समूह) का बोध होता है, मात्रा सूचक कहलाते हैं।
उदाहरणार्थ:- (a) सप्ताह में 7 दिन होते हैं।
(b) कक्षा 7 में 70 विद्यार्थी हैं।
कुछ महत्वपूर्ण प्रश्न
प्रश्न – प्राकृत संख्याओं को प्राकृतिक संख्याएं (Natural Numbers) क्यों कहते हैं?
उत्तर – महान गणितज्ञ क्रोनर के अनुसार प्राकृतिक संख्याएं भगवान (प्रकृति) की देन है, इसलिए प्राकृत संख्याओं को प्राकृतिक संख्याएं (Natural Numbers) कहा जाता है।